
原创 David Krakauer 集智俱乐部

导语
复杂性科学和机器学习是两个密切相关的领域,都致力于在高维、不可还原的现象中寻找模式。复杂性科学采用了粗粒度的理解范式,关注的是大规模的、宏观的模式和趋势。相反,机器学习采用了一种细粒度的预测范式,试图通过学习大量数据中的细微模式来进行预测。近日,圣塔菲研究所所长大卫·克拉考尔撰文,尝试从理论层面实现复杂性科学与机器学习的统一。文章认为,两种方法都试图解决“维格纳逆转”,即在处理复杂现象时,简单的数学模型无法像在物理学中那样有效。同时,它们也试图解决数学在自适应领域(普遍存在对称性破缺和遍历性破缺,涉及大量参数和复杂动力学行为)的低效问题。这就需要我们使用“元奥卡姆剃刀”,即任何能够发现新形式的、富含模式的有效理论的简洁过程或算法。
研究领域:复杂科学,机器学习,物理模型,统计模型,模式
David C. Krakauer | 作者
郭瑞东、王朝会 | 译者
刘培源 | 审校

论文题目:
Unifying complexity science and machine learning
论文地址:
https://www.frontiersin.org/articles/10.3389/fcpxs.2023.1235202/full
目录
一、复杂模式和统计流形
二、维格纳逆转和费曼极限
三、奥卡姆剃刀 vs 元-奥卡姆剃刀
四、在“超休谟”模型中发现模式
五、结论
复杂性科学(Complexity science)与机器学习(Machine learning)是发现并编码不可约的高维现象中隐含规律的两种互补方法。其中,复杂性科学为我们提供了一种粗粒度的理解框架,而机器学习则呈现出一种细粒度的预测范式。这两种方法都在试图解决“维格纳逆转”(Wigner-Reversal)问题,也就是数学在自适应领域中显得不合理且无效的情况,该领域主要被对称性破缺和遍历性破缺所主导。为了融合这些范式,我提出了“元奥卡姆”的思想,它 1)将最小化原则从描述现象模型转向描述生成模型过程,并2)描绘出这些模型中低维度特征——模式(schema)。在这个修订后的最简过程概念中,强化学习和自然选择都表现出其简洁性,它们参数化包含潜在低维规律的任意高维归纳模型。我将这些模型称为“超休谟”,并探讨分析其潜在维度——作为功能模式编码——的科学价值。
一、复杂模式和统计流形
数据驱动的知识发现过程类似于一个序列,从感知和测量开始,最终得出概念和规则。哲学家伊曼努尔·康德(Emmanuel Kant)在1781年的《纯粹理性批判》中将感官印象(直接或以工具为媒介的)到概念的映射描述为模式(schema)的产生。模式是将丰富的输入数据转化为抽象范畴的规则,其中范畴是思想、理论和科学的基础。
约翰·霍兰(John Holland)和默里·盖尔曼(Murray Gell-Mann)在对复杂系统下定义时,采用了康德关于模式的思想。在霍兰看来,模式是一个二进制字符串,可以用固定元素(而非通配符)来定义适应性景观中最优解的等价类坐标。对霍兰来说,复杂系统的组成实体具有类似的模式。对盖尔曼来说,模式,他也称为信息收集利用系统(IGUS,Information Gathering Utilizing System)是一种压缩的规则系统,能够接受来自历史和环境的信息输入,从而做出预测和行动。这种定义适用于基因组、神经系统,甚至物质文化领域。在这种情况下,模式类似于“代码生物学”(code biology)对代码的强调,代码生物学将文化和生物学作为两个表征领域,研究从句法标记到语义符号的映射。詹姆斯·哈特尔(James Hartle)将信息收集利用系统形式化,通过将其放置在闵可夫斯基空间中,来追溯“主观”世界线的出现,从而来探索新概念的起源,例如现在、过去和未来。这样,复杂性(具有主体性的生命)和简单性(变分物理学)就连接起来了。可以说,复杂的现实是由编码系统演变来的,编码系统中还保留了其适应历史的粗粒度记忆或存档。而物理学中的基本对称性,反复被具有非遍历特性的规则系统覆盖。
模式和数据科学中的流形(manifolds)概念非常相似,它是一种低维的几何编码可以捕捉高维数据集中的稳定关系。在从“测量”到“概念”的过程中,机器学习算法会不断地改变向量空间,来发现简约流形。这样一来,神经网络中的学习看起来就是在计算霍兰或盖尔曼定义的模式,从而直接从数据中构建复杂系统。我们的目的就是从这些压缩的模拟中提出科学化的解释。
复杂性科学和机器学习是从具有丰富模式的现象中进行发现的两个较为成功的工作。它们的研究对象不是物质实体本身,而是具有目标导向的物质(例如生物体等)。这两种方法都被认为能够为各类现象提供洞察和预测,这些现象包括反射性系统或主体性系统,它们能够对历史数据集进行编码来进行适应性决策。一个悬而未决的问题是,机器学习是否真的能够发现这种自适应模式。最近的几项研究工作提供了一些线索,说明了机器学习中可能会遇到的一些挑战,以及为了使纯粹的关联模型能够生成可理解的输出,需要在其中加入哪些人类思想和约束条件。这些要求可以概括为先验、约束和策略三种。这些都限制了构型空间,来增强归纳过程。
(一)需要基于知识的先验
神经网络是一种通用的函数逼近器,可以通过训练来模拟动力系统。显而易见的方法是在网络中对运动的二阶微分方程进行潜在编码,并输出速度和动量,以符合任何所需的轨迹。在大型的非线性动力系统中,这意味着会使用一个相当复杂的奖励函数,并需要对所有相关自由度提供梯度信息。另一种方法是利用物理约束。在这种情况下,哈密顿力学的形式利用了可微流形和辛几何的知识。在最近的研究中,米勒(Miller)及其同事比较了通过哈密顿反馈利用守恒定律的先验知识训练出来的网络和那些没有利用物理学对称性先验知识的网络。对于线性和非线性振荡器,哈密顿神经网络(HNNs)在系统规模上的扩展远比普通的神经网络更有效。因此,对于纯粹关于相关性的机器学习模型来说,了解最小作用量这一基本的物理原理,可以使得奖励信号更简洁和稳健,从而提高模型性能。
(二)编码现实数据的稀疏性约束
许多自然信号,包括视觉数据和声音数据,都有一个有据可查的事实,那就是它们在信息上是稀疏的,可以在不损失信息的情况下,消除很多信号。这就是图像(如 JPEG)和声音(如 MP3)的有损压缩技术得以实现的原因。压缩感知技术可以将大规模的机器学习的关联数据集(R(m)中的向量),缩小为更小的数据集(R (n) 中的向量,其中n ≪ m)。这些稀疏数据的编码是由一组系数相对较少的正交基(如傅里叶基)决定。可以对大规模的稀疏数据集在选定的正交基上进行投影,来压缩信号。已经证明,通过使用合适的最优压缩感知算法,可以使得n ≈ N log(m)。因此对基的先验知识可能会显著加速关联学习的过程。
(三)策略常识
模式丰富的系统有一个有趣的特点,是它们可以内部编码其他模式丰富的系统。一个典型例子是贝叶斯博弈中的协调问题,玩家之间可能存在或不存在共同的先验知识,也就是共享的模式。贝叶斯博弈是不完全信息博弈,不同的玩家拥有不同的私人信息。这些私人信息和正在进行的特定子博弈相关。博弈由多个子博弈(例如正态形式双矩阵博弈等)组成,这些子博弈由被称为“自然选择”的随机事件选择。自然选择的类型存在分布。子博弈内的行动根据自然选择的行动和信息得到相应的博弈结果。例如,玩家可以玩合作博弈(CG)或囚徒困境博弈(PD)。这两个子博弈的行动是共享的知识(合作和背叛),但根据选择的子博弈,回报会有所不同。在一次博弈中,合作博弈会倾向于合作,而囚徒困境博弈会倾向于背叛。德克尔(Dekel)和他的同事认为,如果自然选择的分布没有被共享(共同的先验知识),那么最优的贝叶斯学习者将无法学习到子博弈中的混合纳什均衡。这表明,基本形式的先验“社会知识”可能会增强策略性部署的机器学习。
二、维格纳逆转和费曼极限
恩斯特·马赫(Ernst Mach)在《科学的经济性》中指出“能够以最经济的方法发展的科学是那些其事实可以归纳为少数性质相同的可计量的科学。这就是力学,在其中只涉及空间、时间和质量。”并且“数学可以被定义为计数的经济学”。在科学革命过程中经济简约的推理方法的成功,使得阿尔弗雷德·诺思·怀特海(Alfred North Whitehead)打趣道:“17世纪科学的历史读起来就像是柏拉图或毕达哥拉斯的一个生动梦境”。
尤金·维格纳(Eugene Wigner)在1960年发表的一篇题为《数学在自然科学中不合理的有效性》论文中对具有最大解释力的最小数学做出了权威性的阐述。他描述了数学模型在解释经典力学下行星运动以及量子力学下的复杂光谱和兰姆位移的成功,并提出了认识论的“经验”定律。这条定律描述了数学的演绎规则和物理定律之间惊人的对应关系。
数学哲学家马克·斯坦纳(Marc Steiner)进一步完善了维格纳的洞察,将这一认识论定律解释为物理现象和数学结构之间存在某种内在的类比关系。例如,数学的线性性质可以类比于物理的叠加现象,关键的要求是,物理过程要有规律可循,能够用相对简单的命题来描述。
当我们面对复杂的现实问题时,维格纳的认识论定律就会瓦解。在生物学、人类学或经济学中,很少有一种简洁的数学理论能与数学物理学理论中的数值精确度相媲美。维格纳的洞察实际上被颠覆了,至少以物理学的标准来看,数学似乎在复杂领域是不合理地无效(见图1)。对于“维格纳逆转”的部分答案在理查德·费曼(Richard Feynman)在他的《物理学讲义》中提及,他问了在物理学中理解某个事物意味着什么:
“我们可以想象,构成“世界”的这一系列复杂的运动着的事物,就像是众神正在下的一盘大棋,而我们是这盘棋的旁观者。我们不知道比赛的规则是什么,我们能做的只是观看比赛的进行……当然,如果我们观看的时间足够长,我们最终可能会明白其中的一些规则。比赛的规则就是我们所说的基础物理学。然而,即使我们知道每一条规则,我们也可能无法理解游戏中为什么要走某一步棋。这仅仅是因为比赛过于复杂,而我们的思维有限。”
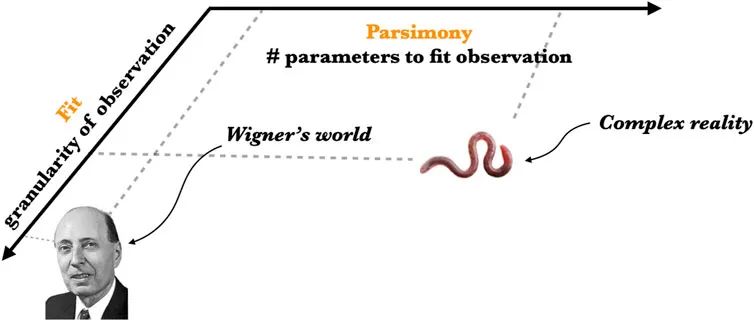
图1 维格纳的世界:基本物理理论通过简洁理论与可观测量实现细粒度的拟合,这就是尤金·维格纳所描述的“数学的不合理有效性”。复杂的现实:复杂的世界无法达到这种程度的命题压缩,需要更大的模型(更长的描述)来对可观测量进行粗粒度的拟合。
复杂现实的主要特征是,它虽然遵循物理定律,但不是由物理定律决定的。正如安德森(Anderson)在他的奠基性论文《多者异也》(More is Different)中明确指出,复杂性的本体论特征是一系列的对称性破缺,也被称为“冻结的意外”,这些对称性破缺在生物和文化进化过程中逐步累积。这些破缺的对称性对于适用于遍历系统的简约数学的能力施加了一个非常严格的上限。可以说,复杂的现实已经超出了我称之为“费曼极限”的范畴,其中对现实世界的理解被具有决定性的非遍历的“行动”所主导,超出这个范畴后,物理规则和定律就失去了很大的解释力。复杂的现实朝着不可还原的高维度和复杂性演化,几乎没有马赫的“计算的经济性”或怀特海的“毕达哥拉斯的生动梦境”,更像是林奈的历史加密自然史。
三、奥卡姆剃刀 vs 元-奥卡姆剃刀
尽管复杂性表面上是不可简化的,但复杂现象的一个耐人寻味的特征是,描述性和预测性模型的信息含量很高,而生成相同模型的过程的信息含量却很低。基因组和深度神经网络的高信息含量,和相对简单的自然选择(NS)和强化学习(RL)的低信息含量,就是两个很好的例子。自然选择和强化学习都可以用于进化或训练任意复杂的主体和模型。换句话说,细菌或哺乳动物进化的达尔文逻辑本质上一致,训练简单分类器和大型语言模型的强化学习方案也是如此。从拟合观察结果所需的众多参数来看,存在着维格纳逆转,但从生成过程的少量参数来看,却伴随着惊人的简单性。奥卡姆剃刀不适用于复杂系统,但我们可以称之为元-奥卡姆剃刀,适用于构建复杂系统。我们需要的是一种历史进程,它能够打破对称性,并将这些对称性存储在合适的记忆中。这些过程的一个结果是,它们通常会产生模式(基因、电路、模块),这些模式是对模型所处世界的粗粒度反映的编码。我们应该把元-奥卡姆剃刀视为一种能够发现丰富模式的有效理论的简约过程或算法。
这凸显了复杂性科学和机器学习与基础物理学之间的根本区别。在基础物理学中,奥卡姆剃刀适用于物理现实的结构(例如标准模型),而试图解释标准模型的理论,包括解决“微调问题”的方案,往往是无限复杂的。这些理论包括多元宇宙理论(我们从中选择自己的宇宙的无限多样性),自上而下的宇宙学(初始条件的无限多样性),和模拟理论(弱人类原理的无限回归)。图2举例说明了这种情况,复杂现实映射到非简约模型和元简约过程(P2),而物理现实映射到简约模型和非元简约过程(P1)。
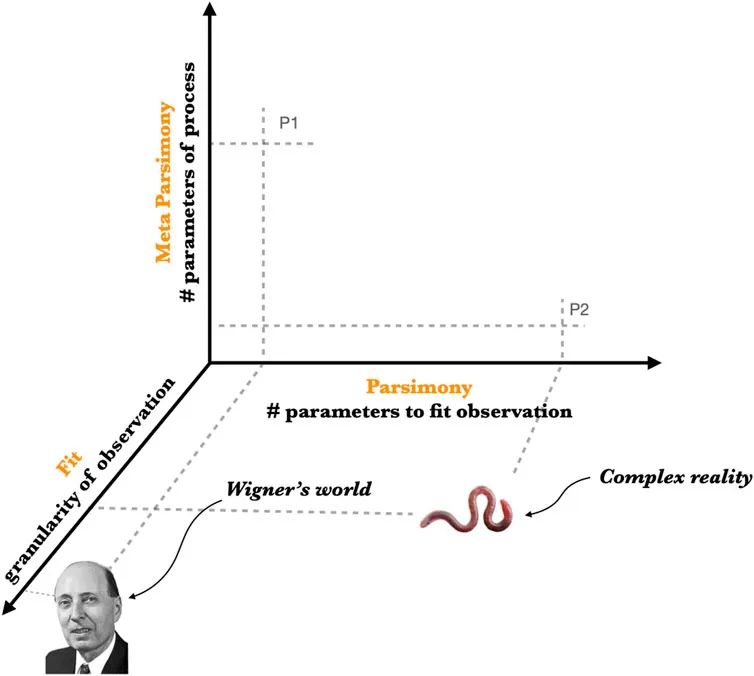
图2 维格纳的世界在可观测层面上是简约的,但在起源上远非简约。这些世界背后的过程通常被描述为物理现实的微调是非常大的(P1),或者在复杂性上实际上是无限的。复杂的现实并不简约,而是元简约(P2)。像自然选择和强化学习这样的过程可以扩展到任意大的模型。因此,物理知识和复杂知识在不同的解释领域实现了最小化。
四、在“超休谟”模型中发现模式
要想在理解复杂性方面取得进展,我认为有必要将机器学习提供的细粒度预测范式和复杂性科学提供的粗粒度理解范式进行整合。在图3中,我将理论空间划分为四个象限,分别由模型参数和现象维度两个维度来描述。物理理论(B),如维格纳和马赫,使用基本参数(如引力常数)来表达低维度规则系统(如引力)。通过寻找更基本的规则,运用对称等原则简化了不必要的复杂模型(A),从而实现奥卡姆剃刀。无法简化的高维现象使用捕捉无数高阶关联的有效参数进行拟合(C),或者用粗粒度的等式描述新出现的模式(D)。在非常大的统计关联中寻找模式,不仅仅是应用奥卡姆剃刀(即消除低于某一阈值的相关性),而是通过自然选择和强化学习等过程,在有效自由度之间发现新的机制。
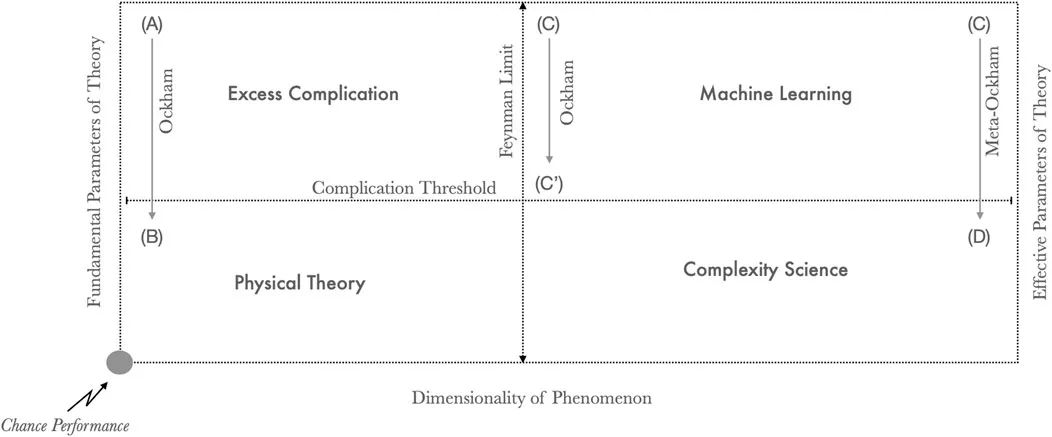
图3 在理论空间上数学的分类。(B):物理理论用少量基本参数描述低维现象。(A):低维现象通常以超过复杂性阈值的复杂理论开始。奥卡姆剃刀被用来将理论转移到简约的物理理论空间(A->B)。(C):可以用大型关联模型描述高维现象,捕捉特征丰富的流形。(C'):可以通过有损压缩来简化模型,从而剪掉亚阈值参数(C->C')。(D):通过使用元-奥卡姆剃刀,在机器学习模型中通过适当的粗粒化的抽象,发现具有有效参数的低维构造。
图4描绘了通过理论空间进行科学发现的可能路径。所有模型是从适当简化组成部分及其相互作用开始的,微观粗粒化(MiC)就是将复杂过程简化为简单组成部分。在种群遗传学中,基因被编码为对全局适应度函数的简单线性或非线性贡献;在物理学中,在特定的场内,粒子的性质被编码为电荷;在博弈论中,主体被编码为策略,相互作用被编码为标量收益。
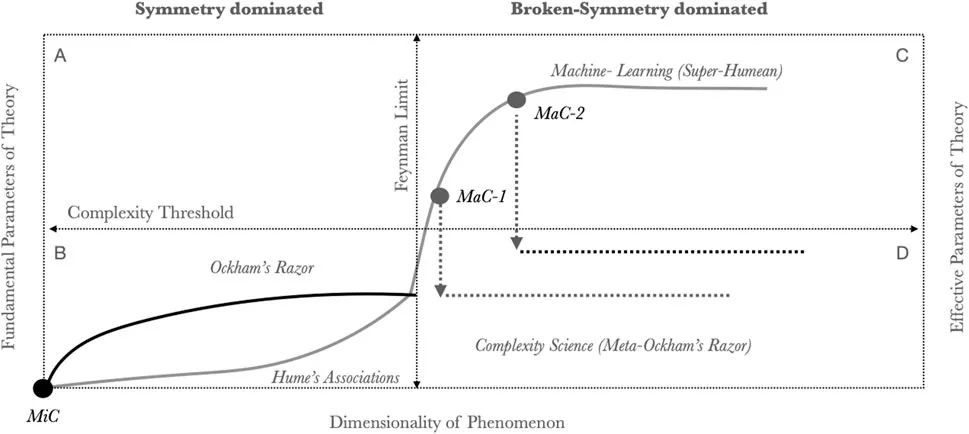
图4. 理论空间中的路径。所有理论都从适当的微观粗粒化(MiC)开始,并随着现象的维度增加而复杂化(象限B)。物理理论通过发现基本对称性使复杂性达到饱和。因此,维度的进一步增加并不伴随基本参数的增加(例如,在多体问题中,万有引力定律会出现局限性)。统计模型通过对参数数量施加适当的惩罚来控制其规模。在费曼极限内,这种缩放仍然成立,一旦达到这个极限,对称性破缺和遍历性破缺而非基本规则主导了系统行为。统计模型在描述或拟合越来越高维度的现象时会无限制地继续增长,而物理模型不再提供信息。超大型统计模型(象限C)实现了对不可还原的复杂数据集的超休谟编码。通过宏观粗粒化(MaC1-2),不同等级的统计模型可以通过发现用因果关系来取代相关关系来近似。MaC-1展示了一个相对较小的统计模型,在这个模型中,模型相关性允许压缩成一个对维度不敏感的机制理论(象限D)。MaC-2描述了只有非常大的统计模型才能进行粗粒化的情况。在这种情况下,只有在训练出合适的超休谟模型后,才能发现新的机制理论。
要探索特定系统的整体特性,总是需要一个合适的微观粗粒化。神经网络模型就是一个很好的例子,在这个模型中,神经元被编码为修正线性单元(ReLU),这些模型训练可以编码非常大的数据集,从而实现前所未有的“超休谟”(以休谟命名,他认为所有知识都是基于关联和名义上的因果机制)归纳性能。这使得我们能够发现在较小模型中不存在的规律。模型扩展和模型性能之间非连续性(模型性能并非随着模型扩展线性平滑提高,而可能是达到一定规模后突然显著提高)的证据已经非常丰富,证据来自超大型神经网络在各种复杂领域取得的显著成功,包括计算机和组合游戏中的表现,视觉分类任务,语言生成,以及在结构生物学中的预测。
有待探索的是如何将这些模型用作复杂性科学理解复杂现实的辅助工具。复杂性科学可以将由简单(微观粗粒化)元素构建的大型统计模型作为输入,以便在其中合适的宏观粗粒化(MaC)。在所有科学模型和理论中,微观粗粒化单元都是假定的,而宏观粗粒化属性则需要被发现。宏观粗粒化的价值在于它们为低维有效理论的发展提供了基础。在图4中,我说明了在统计模型中发现粗粒度模式(MaC1-2)与有效参数的显著减少有关。
物理模型和统计模型都能提供简单系统的简洁描述(象限B)。物理模型通过寻找最小机制来实现,而统计模型通过适当的正则化来实现。当对称性被打破,物理机制开始失去解释能力,系统的非遍历性凸显,此时系统的大部分相空间变得局部化。在超出这个极限后,物理理论仍然有用,但是很少提供的进一步预测。对于统计模型来说,随着维度的增加,有效参数量也会增加。这样可以更好地拟合数据(象限C)。然而,在大型统计模型中发现“有效自由度”是有可能的,这个自由度受任何遵循元-奥卡姆原则的算法来处理和拟合底层数据集的宏观粗粒化影响。这个最小化的过程用于生成具有潜在低维规律的最大化模型。图4展示了两种类型的宏观粗粒化,包括MaC-1(适度统计模型中的模式发现)和MaC-2(超休谟模型中的模式发现)。
(一)MaC-1中的模式:潜在状态
自动编码器和变分自动编码器通过利用强化学习,学习未标记数据集中的嵌入或潜在空间,提供了压缩数据集的方法。线性自动编码器实际上是在解决类似主成分分析的简单特征值问题。和普通自动编码器相比,变分自动编码器通过添加明确的正则化条件(最小化相似性损失),可以在潜在空间对数据进行更连续平滑的编码。用本篇文章的语言,自动编码器就是在数据集中发现宏观粗粒化。有了这些宏观粗粒化,就像主成分分析一样,可以用较少的潜在变量来表达有效的理论。而因子分析技术,包括主成分分析,在选择变量和观察顺序上非常敏感,而自动编码器则更加稳健。
在最近的研究中,探索变分自编码器中瓶颈效应的影响时发现,基于信息瓶颈的粗粒度训练能够高效地发现潜在空间,可用于表示手写数字和街景房屋编号的典型视觉图像中。在输入从语音中提取的声学信号的神经网络中加入瓶颈自编码器,也发现了类似的结果。这两项研究都说明了统计模型是如何实现的,一是通过简单的算法进行训练,二是通过操作以获得低维数据的编码。这些编码成为更传统的机制模型的基础。只要基础特征是“真实世界”系统所使用的特征,增加数据集的大小不会增加这些模型的维度。一个非常好的例子是,使用符号回归从图神经网络中提取暗物质动力学的代数规律。这个项目将带有偏差的物理领域或物理问题(粒子相互作用)与网络结构(相互作用图)对齐,然后找到封闭形式的可解释的表达式,捕捉数据中的规律性。
(二)MaC-2中的模式:生物特征和单位
生命系统发现了在非常复杂的环境中适应和行动的方法。构建模式就是这种能力的一个重要方面,它能够以非平凡的方式生成独立的功能特征。当对细胞和神经系统分析时,如果不是关注细节层面的化学和感官输入,会发现它们都具有一系列高效、可组合的低维度和机械单元,这些单元可以组合成适应性功能。在超大型分子化学数据库进行强化训练得到的循环神经网络,能够生成理想化的、高度粗粒化的分子(模式分子),可以用原子的连接序列进行描述。这些模式分子能够生成和现实世界中分子相似的性质分布。然后,可以通过从这些分布中选择合适的属性并提取相关的“模式分子”,来发现新的分子。因此,大型数据集可训练生成式神经网络,从而发现分子的基本特征,这些特征成为更传统的化学模型的粗粒化基础。就像理想化分子(例如字符串)是一种诱导模式,机器人肢体在空间中产生的动态轨迹也是一种诱导模式。在大型真实世界的动态图像数据集上训练的空间自编码器,能够通过强化学习获得紧凑的状态空间,这些状态的激活能够得到高效的操控机器人的路径。因此,通过引入适当的宏观粗粒化过程,超大型机器学习模型可以对数据进行预处理,有助于低维机制理论的构建。
五、结论
我认为,从根本上来说,机器学习和复杂性科学都是在追求功能模式。它们都研究编码自适应历史的机器结构——从分子传感器到语言游戏。幸运的是,它们以互补的方式进行研究,我们可以将其视为机器学习对现象的预处理(编码为非平凡的依赖关系),以及复杂性科学对编码的后处理(粗粒化为模式)。粗粒化通过揭示系统中的自然单位,可以提高计算效率,限制组合爆炸,能够分析长时间尺度的行为,阐明因果关系,并为非线性时间序列提供有原则的压缩。
科学革命为此提供了一种有用的类比,例如科学仪器和科学理论之间的关系。光学望远镜捕捉并聚焦可见光波长,并将其作为输入提供给简化的数学理论,例如轨道理论。而广义相对论等简化理论则允许根据独立于光学无关的原则设计引力波探测器。如果我们将机器学习看作是算法望远镜,并熟悉其操作模式,那么就有可能为那些通过更直接的观察,在被证明无法简化的嘈杂领域发现全新的规则和法则。通过元-奥卡姆过程,大型统计模型可以为复杂领域的全新机制理论奠定基础。
原标题:《前沿综述:统一复杂性科学与机器学习》